About Function Definition:
A relation is a set of ordered pairs (x, y). When each x-value in the set is linked to exactly one y-value, that relation is called a function. In a function, no x-value can correspond to more than one y-value. In other words, each input (x) is paired with a single, unique output (y).
Test Objectives
- Demonstrate the ability to determine if a relation is a function
- Demonstrate the ability to find the domain and range of a relation
#1:
Instructions: Determine if each relation is a function.
a) {(-6,-3),(2,4),(7,1),(8,9)}
b) {(-2,6),(3,4),(3,-1),(7,-11)}
Watch the Step by Step Video Solution View the Written Solution
#2:
Instructions: Determine if each relation is a function.
a) {(-1,-1),(3,7),(8,-8),(6,4)}
b) {(12,3),(6,9),(9,6),(1,4)}
Watch the Step by Step Video Solution View the Written Solution
#3:
Instructions: Determine if each relation is a function.
a) {(2,1),(17,6),(9,6),(-4,8)}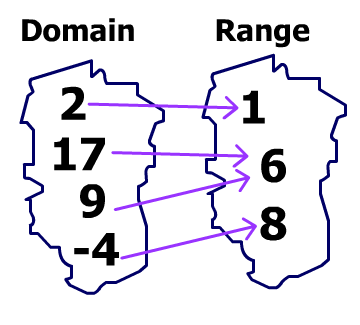
b) {(5,-8),(5,6),(3,1),(7,4)}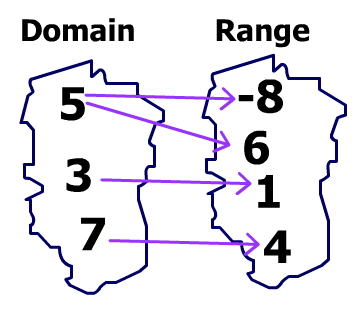
Watch the Step by Step Video Solution View the Written Solution
#4:
Instructions: Use the vertical line test to determine if each relation is a function.
a) {(-1,7),(1,1),(2,-3),(3,0),(7,5)}
Watch the Step by Step Video Solution View the Written Solution
#5:
Instructions: Use the vertical line test to determine if each relation is a function.
a) {(-3,7),(-3,2),(-1,3),(1,1),(2,3),(4,6),(6,1),(6,-2)}
Watch the Step by Step Video Solution View the Written Solution
Written Solutions:
#1:
Solutions:
a) Function
b) Not a Function
Watch the Step by Step Video Solution
#2:
Solutions:
a) Function
b) Function
Watch the Step by Step Video Solution
#3:
Solutions:
a) Function
b) Not a Function
Watch the Step by Step Video Solution
#4:
Solutions:
a) Function
Watch the Step by Step Video Solution
#5:
Solutions:
a) Not a Function